Hey @gpkesley, thanks for suggesting svbtle.com!
I like how it’s so streamlined. A dark colour scheme would be easier on the eyes, but otherwise the design is pleasing.
Here are the first couple of posts.
http://lrnjrnl.com/why-lrnjrnl
http://lrnjrnl.com/designing-an-interpreter
No worries. I’ve subscribed via RSS feed.
That is some deep s**t your into mate!
Thanks. It’s crazy how much work it takes to come up with the solutions that we all take for granted.
BTW, that’s a neat logo you’ve got.
I bet.I suppose its an evolution over time though too. I think its very impressive what you are doing.
Thanks on the logo. Its my corporate logo from my WordPress site that doesn’t get much airtime so I thought I’d use it more. Shameless plug: http://www.ashtreeitsolutions.co.uk
I tried implementing function calls using this ‘stacked’ lexical, local scopes idea I had. It might be impossible to pull off like this because what I want is to be able to store function definitions (and their respective environments) in variables in the symbol table). To do this, it turns out I do need closures. That is, I need to copy the environment variables to a symbol table which gets bundled with the function’s code. This is what gets assigned to a variable, passed as a parameter or returned from another function.
It turns out there is a name for this: first class functions. According to wikipedia, this feature was first implemented in a language called Scheme. I’ve found a few a couple of Scheme-building tutorials:
https://en.wikibooks.org/wiki/Write_Yourself_a_Scheme_in_48_Hours
http://peter.michaux.ca/articles/scheme-from-scratch-introduction
I don’t think I’m ready to start either of these tutorials, but I may come back to one of them if I ever need to learn functional programming.
I predict you will be writing your on Scheme in C by the end of the month.
I think I’ve found a more elegant way to implement closures. Rather than copying all the values of the free variables into the (function_code, function_scope) bundle in the symbol table, the interpreter can use a CALL STACK! The stack frame for the current function’s local scope will reference the enclosing/parent function’s scope in a frame which is FURTHER UP THE STACK (not to be confused with the calling scope’s frame). My guess is that this would be much faster (fewer assignments) and less memory intensive (no multiple copies of a variable for each function call).
Each stack frame will have a ‘self.encloser’ attribute which will point to the enclosing function’s stack frame. Together, these stack frames will form a kind of linked list (or an inverted tree?) which leads all the way up to the root scope.
The stack will be kept in the interpreter object and will interact with the FuncCall class when pushing and popping frames (and hopefully passing arguments and returning values).
I’ve already started writing a blog post that goes into more detail, but I really want to make diagrams to communicate the idea. I think it should be pretty straightforward. Right now, the classes are still being written. So I might wait to make the blog post once the implementation is nearly crystallized.
Implementing first class functions has been a struggle. I’m hoping that this strategy will let the interpreter reuse some visit methods that were written the analyzer. Fingers crossed!
Oops. I’m running in circles!!
I thought it through some more. I still need to copy the values! Otherwise, if function inside() has a free variable x will change whenever x gets reassigned in the enclosing scope… say outside().
Here’s what I’m picturing
def outside():
x = 5
def inside():
print("hello from inside! x==", x)
inside()
x = 3
inside()
If I were to use this ‘stack’ idea to handle closures, I would first see the message
>>> "hello from inside! x==5
and then
>>> "hello from inside! x==3
That’s definitely not what I want!
The output from inside() should always be
>>> "hello from inside! x==5
So it’s back to copying values for closures!
I’m still working on the blogpost to explain the call stack because I still need it to make my interpreter work properly.
Awesome, so are you going to continue with the rest of the book or have I created a monster?
I still plan on getting through the database part once I complete part 4. I’ve slowed down a lot with work and family commitments, but I’m getting my groove back now.
That said, coding a Scheme in c has definitely piqued my interest. I was planning on building a web portfolio, but the attraction of CS is strong. So much so that I’d like to review calculus and take it in university in 2019.
MY INTERPRETER PASSED THE FIRST TEST!!!
Celebration time! I finally got my entire interpreter to pass a test. Here are the links… the scripts all go in the same folder.
Please ignore the comments in the code. They are totally messed up because I wrote them and then made many changes. I might rewrite them later.
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/scanner.py
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/parser.py
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/productions.py
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/analyzer.py
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/interpreter.py
https://lab.learncodethehardway.com/austen/lmpthw_solutions/blob/2aa3211c8da48487c80768b0ab89c253cc8a56f8/part4project/test_interpreter.py
here’s the test:
#!/usr/bin/env python
import interpreter
TOKEN_MAP = [
("DEF", r"^def\s"),
("RETURN", r"^return\s*"),
("NAME", r"^[_A-Za-z]+[_0-9A-Za-z]*\s*"),
("LPAREN", r"^\(\s*"),
("INTEGER", r"^[0-9]+\s*"),
("COMMA", r"^,\s*"),
("RPAREN", r"^\)\s*"),
("COLON", r"^:\s*"),
("PLUS", r"^\+\s*"),
("ASSIGN", r"^\=\s*"),
("INDENT", r"^\s+"),
]
CODE_SAMPLE = """def hello(x, y):
print(x + y)
hello(1, 2)
hello(3, 4)
a = 5
b = 6 + 7
c = a + b
a + b + c
hello(a, b)
"""
def main():
code = CODE_SAMPLE.split('\n')
print("VVV CODE STARTS BELOW VVV")
for line in code:
print(line)
print("VVV OUTPUT STARTS BELOW VVV")
terp = interpreter.Interpreter(TOKEN_MAP, code)
terp.interpret()
if __name__=="__main__":
main()
…and here’s the output:
bash-4.4$ ./test_interpreter.py
VVV CODE STARTS BELOW VVV
def hello(x, y):
print(x + y)
hello(1, 2)
hello(3, 4)
a = 5
b = 6 + 7
c = a + b
a + b + c
hello(a, b)
VVV OUTPUT STARTS BELOW VVV
3
7
18
I didn’t directly use a stack, but I took Zed’s World idea and called it a ‘CallFrame’… The CallFrame doubles as a container for closures, but essentially, the call frames are the containers in which function calls create local scope for the callee. While this isn’t a stack per se, it has a similar effect. I could even pop CallFrames off the ‘stack’ by using del after the function returns to ensure there’s no wasted space. But maybe python’s garbage collection already takes care of that for me. 
I also figured out that, even though a dictionary has to be copied for each scope, the copies are only pointers/references! This means that there aren’t multiple copies of each object accumulating as you go down the stack.
What’s missing? Conditions. If I built conditions, I could make a real programming language with loops and recursion. But I think I’ve spent enough time on this language for now. Once I revise the commenting, I’ll go on to the next exercise and hopefully finish part 4 of LMPTHW.
…but I am still itching to build the conditions!!
So what do I think? It’s definitely some messy code! There’s a lot of redundancy and inconsistent design choices because I HAD NO IDEA WHERE IT WAS GOING! But now that I’ve built an interpreter start to (almost) finish, I could definitely find ways to smooth it out. The point is: By struggling through this exercise, I learned a hell of a lot about computers.
Thank you @zedshaw 
I updated the test to account for first class functions. It broke the analyzer!!! After an hour of tweaking the visitor methods for variable assignment and lookup, I got it working and noticed that the analyzer was the only part affected. The interpreter was already completely capable of assigning a function to a variable and then calling it!
Here’s the new version of the test output:
ash-4.4$ ./test_interpreter.py
VVV CODE STARTS BELOW VVV
def hello(x, y):
print(x + y)
hello(1, 2)
hello(3, 4)
a = 5
b = 6 + 7
c = a + b
a + b + c
hello(a, b)
goodbye = hello
hello = 0
goodbye(c, c)
VVV OUTPUT STARTS BELOW VVV
3
7
18
36
Debugging the analyzer made it obvious that there’s a lot of cleaning up to do in there, but it also made me happy that the interpreter is fairly robust when it comes to handling functions in assignments and expressions.
I’m planning to go back to university where I’ll be able to study calculus. I found this blog post very encouraging not just for math, but for programming too.
Get this book:
It’s 100+ years old but still the best book on Calculus. It taught me a lot about how to teach complex subjects gradually. Then get any book of Calculus problems so you can practice solving them.
You can also find updated versions of the Thompson book on Amazon.
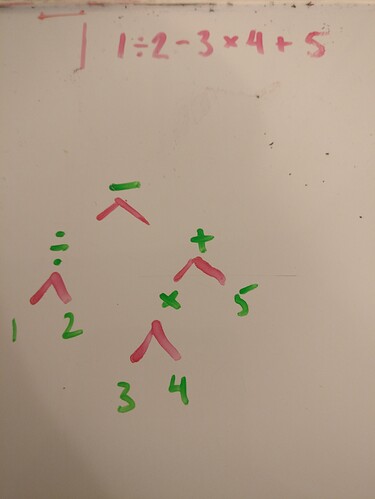
I’m working on the calculator, bc clone. So far so good. I was taking a break from building my parser when I saw this video on algorithms that teach math. One of the slides was a parse tree graph of an arithmetic expression! I studied the lecturer’s slides and started playing with different expressions to see if I could consistently get it to represent operator order. It works!
This structure had been floating around in my head, but it has been difficult to implement because I would get lost in the details. This graphing method makes it so much easier to keep track of the grammars.
Here’s the video
I’d like to point out that this is pretty much exactly the same as the binary search tree, except with order of operations. It’s all left-side, right-side expression nesting.
Oh Zed. I bet you had this planned all along.